월간전기



[독자 칼럼]전기기기 설계-직류기와 변압기 설계를 중심으로⑩

2018-12-01

일본의 다카하시(高橋辛人) 박사의 저서를 편역한 배진용 공학박사(동신대학교 전기차 제어 교수)의 열 번째 연재를 이어간다. 지난 호부터 게재하는 2장 31챕터의 ‘300kW 직류발전기의 설계 예’는 ?전기자 주요부분 설계와 ?정류자 및 브러시의 설계, ?계철 및 계자의 설계, ?공극의 암페어 턴수(AT) 계산, ?전 부하 암페어 턴수(AT) 계산, ?분권 계자설계, ?직권계자 설계, ?보극의 설계, ?손실의 계산, ⑩기타 손실, ⑪효율 계산, ⑫온도상승 계산, ⑬분권 계자권선의 온도 상승 등으로 구성돼 있다. 이번 호에는 ?~⑪번을 소개한다. <편집부> 공극의 암페어 턴수(AT) 계산 공극의 암페어 턴수(AT)는 계철 부분과 다르게 계산한다. [그림 2.56]과 식 (2.26)에서 ‘s/δ = 10/5 = 2f = 0.72’ 에서 카터계수(Cater coefficient)는 다음과 같다. 따라서 공극의 암페어 턴수(AT)는 다음과 같이 계산할 수 있다. AT = 0.8 · C · δ · Bg = 0.8 × 1.16 × 0.5 × 8,310 = 3,860 전 부하 암페어 턴수(AT) 계산 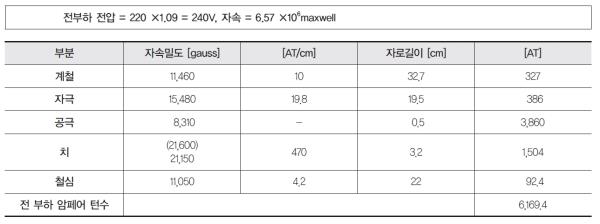위의 표에서 치의 자속밀도 중 괄호는 겉보기 자속을 나타내며 규소강판으로는 S23F를 사용한다. 또한 식 (2.29)의 수치를 만족하는지 확인하여야 한다. 따라서 ‘매극(공극+치)의 AT’를 ‘매극의 전기자 AT'로 나누면 0.828 이므로 식 (2.29)를 만족한다. 식 (2.16)에서 무부하의 경우 ‘k = 1’로 하여 자속을 구하면 다음과 같다. 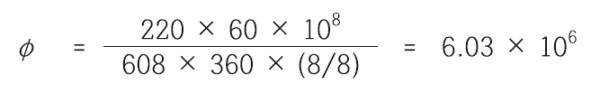분권 계자설계 식 (2.30)에서 L_sh와 ρ를 알면 단면적 A를 구할 수 있다. L_sh를 구하기 위해 분권계자 코일을 권선한 이후의 코일 두께를 30㎜로 가정하면 [그림 2.83]과 같이 분권계자 권선의 단면을 구할 수 있다. 여기서 철심과 코일사이의 절연 두께는 4㎜로 한다. *L_sh* = [(310 + 4 × 2 + 30) + (170 + 4 × 2 + 30)] × 2 = 556 × 2 = 1,112㎜ 여기서 ρ는 계자조정기의 여유를 나타내는 정수로 ‘ρ = 0.769’로 하면, 분권계자의 단면적은 식 (2.30)에 의해 다음과 같이 계산할 수 있다. 전선의 단면적 5.039㎟로부터 권선의 직경을 계산하면 ‘π × r² = 5.039㎟’이고, 여기서 r은 권선의 반지름이므로 권선의 지름은 다음과 같다. 따라서 분권계자 권선은 직경 2.6㎜, 단면적 5.039㎟인 AIW 전선으로 선정한다. 분권계자 권선의 두께를 30㎜로 할 때 측면은 [그림 2.84]와 같으며, 분권계자 권선의 높이는 180㎜가 된다. 분권계자 권선의 절연을 DCC로 할 때, ‘권선의 외경 = 2.97㎜’(권선의 외경은 부록 피복선의 외경 표 참조)이다. 20℃에서 분권계자 권선의 저항 Rsh는 다음과 같다. 이를 75℃로 환산하면 다음과 같다. 직권계자 설계 직권계자 권선의 턴수는 다음과 같다. 이는 거의 1이라 할 수 있다. 따라서 턴수를 2회로 하여 2병렬로 하면 전선 단면적을 작게 할 수 있으며, 공작에 편리하게 된다. 직권계자 권선의 턴수에 소수점이 포함되는 경우 소수점 이하를 올림하여 1회로 한다. 계자 권선에 병렬 저항을 분류기로 삽입하여 턴수를 적절히 조정하는 경우도 있다. 또한 주 자극의 공극을 다소 조정하는 경우도 있다. 직권계자 권선을 흐르는 전류는 1364/2 = 682A일 때, 도체로 7.5 × 40㎜(단면적 298㎟)의 평각선을 선택하면, 전류밀도는 ‘682/298=2.29A/㎟’이다. 권선은 테이프를 반 중권으로 권취하며 두께의 치수는 7.9㎜로 한다. [그림 2.85]는 직권계자 권선의 단면을 나타내며, 이로부터 직권계자 권선의 평균 길이 L_s[㎜]를 구하면 ‘L_s = [(378 + 4 × 2 + 7.9) + (238 + 4 × 2 + 7.9)] × 2 = 1,295.6’가 된다. (P/2)극에 해당하는 저항 R_s′는 다음과 같다. 보극의 설계 보극의 공극은 ‘1.5 × δ = 1.5 × 5 = 7.5㎜’으로 주 자극 공극의 1.5배로 한다. 보극의 폭(Wi)은 ‘λ + s = 20.7 + 10 = 30.7㎜’이나, 적당한 정수인 ‘W_i = 32㎜로 선택한다. 2가닥을 병렬로 하여 13회 권취하면, 6.5회에 상당하므로 이 계산은 적합하다고 할 수 있다. 보극의 길이는 L_c와 같도록 하며, [그림 2.86]은 보극 철심의 치수를 나타낸다. 보극 권선의 치수는 7.5 × 40(단면 298㎟)로 선택하며 간격은 5.5㎜ 평타권(平打卷)으로 한다. 따라서, 보극 도체의 전류밀도는 다음과 같다. [그림 2.87]은 보극 권선의 코일 단면을 나타내며, [그림 2.88]은 보극 권선의 코일 측면에서 도시한 그림을 나타낸다. 보극 측면의 치수는 결정되었지만 이미 결정된 주 자극에 조립하는 경우 계산상으로는 보극 권선이 삽입될 장소에 여유 공간이 있는 것처럼 보여도 실제로는 주 자극과 보극이 중첩되는지 [그림 2.89]와 같이 주 자극 및 보극의 측면도를 그려 확인하여야 한다. [그림 2.87]에서 보극권선 코일의 평균 길이 L_t[㎜]는 다음과 같이 나타낼 수 있다. *L_t* = [(310 + 4 × 2 + 40) + (32 + 4 × 2 + 40)] × 2 = 876㎜ (P/2)극 당 저항 Ri′은 다음과 같다. 20℃에 있어서 보극권선 전체의 저항 R_i는 다음과 같으며, 75℃의 경우 저항과 보극권선의 동손 및 중량 등도 아래와 같이 계산할 수 있다. 손실의 계산 기타 손실 지금까지 손실의 대부분에 대하여 계산하였으나 아직 기계적 손실과 표유부하손에 대한 계산은 이루어지지 않았다. [그림 2.74]에서 기계적 손실은 정격 출력의 2%이므로 이를W로 나타내면 기계적 손실은 ‘300,000 × 0.02 = 6,000W’이고, 앞의 계산에서 브러시의 마찰손(P_b)은 1,214W이므로, 베어링 손실 및 풍손의 합은 ‘6,000 - 1,217 = 4,786W’이다. 그리고 표유부하손은 전류의 제곱에 비례하며, 정격 출력에 상당하는 손실의 1%로 가정하면 3,000W가 된다. 효율 계산 전부하에서 손실은 지금까지 계산한 것을 모으면 다음과 같다. 이상의 손실에서 (1)은 ★f2 I2에 비례, (2)는 I에 비례, (3)은 일정하다. 따라서 (2.41) 식에 나타낸 손실을 다음과 같이 정리할 수 있다. 이와 같은 방식으로 각 부하에서 손실을 계산한다. 상기 손실에 따라 효율을 계산하면 아래 표와 같다. 온도상승 계산 - 전기자에 있어서 온도 상승 계산 D＞40㎝이므로 식 (2.45)에 따라서 온도계에서 31.8℃의 온도 상승을 지시한다면 규격의 보정치 내에 있게 된다. < Energy News >